There are 3 different watershed in Spain:

The Atlantic watershed
The Cantabrian watershed
The Mediterranean watershed

Now that you are an expert, show off your skills with these games.

Bonjour les enfants!!
En el enlace adjunto os dejo el villancico que vamos a cantar para la fiesta de Navidad, así tenéis mas fácil el ensayar. 
Ánimo que lo vais a hacer genial.

JOYEUX NOËL

RELIEF is the shape of the landscape.

Do you remember the relief of our country?

Here you have 2 games to put into practice your knowledge.

If you find that level easy, you should try this game.

Click to watch the video and practice the song

Números enteros  

Algunas características de este conjunto numérico son:

1. El conjunto de los números enteros  está formado por:
   • Los números enteros positivos  : 1, 2, 3, …
   • El cero: 0.
   • Los números enteros negativos     : -1 , – 2, – 3, …
   
   1. Todos estos números conforman el conjunto de los números enteros, el cual se denota por:  = { … , -4, – 3, – 2, -1, 0, 1, 2, 3, 4, … }.
2. Los números enteros negativos se escriben con un signo  delante del número (para indicar que es menor que cero). Cuando un número distinto de cero no va precedido de ningún signo, se entiende que este es un número neutro

Relación de orden

En el conjunto de los números enteros se pueden definir las mismas relaciones de orden que en los números naturales: menor que, mayor que o igual que. Es así que dado dos números enteros cualesquiera, siempre hay uno menor y otro mayor, salvo que ambos números sean iguales.

Signos para comparar

Para comparar números enteros se utilizan los mismos signos que para los números naturales.

Símbolos	Ejemplos
menor que.	– 5  9, se lee “menos cinco es menor que nueve”. – 4  – 7, se lee “menos cuatro es mayor que menos siete”. 2  2, se lee “dos es igual que dos”.
mayor que.
igual.
menor o igual que.
mayor o igual que.

Representación de los números enteros en la recta numérica

Los números enteros se representan de forma ordenada en una recta numérica.
Para representar un número entero en una recta:

1. Se ubica el cero.
2. Los números enteros positivos se ubican (a igual distancia unos de otros) a la derecha del cero.
3. Los números enteros negativos se ubican (a igual distancia unos de otros) a la izquierda del cero.
4. En una recta numérica, será mayor aquel número que se ubique más a la derecha.

Representación en la recta numérica del conjunto .

Valor absoluto de un número entero

El valor absoluto de un número cualquiera corresponde a la distancia de dicho número al punto de origen o cero. Para representar el valor absoluto de un número se utilizan dos barritas verticales. Es decir, el valor absoluto de un número entero a se representa por .

Ejemplo:

, representa tres unidades de distancia al cero. Es decir, .
, representa tres unidades de distancia al cero. Es decir, .

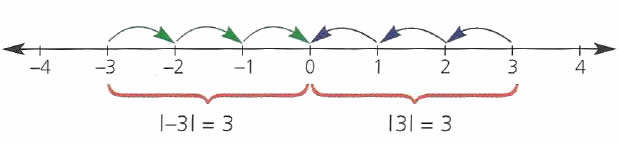
Los valores absolutos de – 3 y 3 son equivalentes, es decir, están a igual distancia del cero.

Valor absoluto de números opuestos

Si dos números tienen igual valor absoluto, pero distinto signo, se dice que estos números son opuestos. Ejemplo: – 5 y 5.

OPERACIONES

PROBLEMAS

• 1. En una estación de esquí la temperatura más alta ha sido de -2⁰ C, y la más baja, de -23⁰ C. ¿Cuál ha sido la diferencia de temperatura?

• 2. Un avión vuela a 11000 m y un submarino está a -850 m. ¿Cuál es la diferencia de altura entre ambos?

• 3. En la cuenta corriente del banco tenemos 1250 €. Se paga el recibo de la luz, que vale 83 €; el recibo del teléfono, que vale 37 €, y dos cheques de gasolina de 40 € cada uno. ¿Cuánto dinero queda en la cuenta corriente?

• 4. Pitágoras nació el año 585 a.C y murió el año 495 a.C ¿Cuántos años vivió Pitágoras?

• 5. Compramos un frigorifico. Cuando lo enchufamos a la red eléctrica está a la temperatura ambiente, que es de 25⁰ C. Si cada hora baja la temperatura 5⁰ C, ¿a qué temperatura estará al cabo de 6 horas?

• 6. He viajado desde San Fernando donde la temperatura era de 11 grados hacia Granada que la temperatura es de 3 grados. ¿Cuál ha sido la diferencia de temperatura?

• 7. Cristian vive en el 4º piso, se sube en el ascensor y baja al sótano 2, ¿Cuántos pisos ha bajado?

• 8. Le debo a mi amigo 10 €. Me ha tocado en la loteria de Navidad 100 €, lo primero que hago es pagarle a mi amigo. ¿Cuánto dinero tengo?

• 9. Tengo en el banco 60 €, me ha llegado una factura de 100 €, ¿cuánto me falta para pagar la factura?

• 10. Si estoy en el piso 2º y bajo 3 pisos ¿en cual me sitúo?

• 11. Un día de invierno amaneció a 3 

Our LOCOMOTOR SYSTEM is consist of skeletal system and muscular system.

Do you remember the bones and muscles?

Here you have a game to remember the bones.

Hello again!

Here we have our first DISCOVERY!

An extra point is waiting for those who guess the question.

We have studied in class that the Earth spend 365 days and... 6 HOURS orbiting the Sun.

We know that a year has 365 days. So... Why every 4 years have we got a leap year (a year with 366 days)?

SOLUTION:

Humans are complex organisms. We are made of basic units of life called CELLS.

All living thing are made of CELLS and have the three life processes.

Earth is our planet, and for us could be huge. But it is not at all in comparison with the rest of the universe.

The universe is made of galaxies. Our galaxy is called the MILKY WAY. Look at it:

To test the effects of living in space, astronauts stay on space station like the International Space Station (ISS). If you want, you can see what astronauts are doing there in this right moment.


"

Hey there boys!!!

Welcome to the new school year! And welcome to the SCIENCE BLOG of 5th grade!

Welcome Back Minions GIF from Welcomeback GIFs

In this blog you will find some interesting videos, photos and games to keep working on the thing we study at school.

La longitud de la circunferencia (o perímetro de una circunferencia) L es igual a dos veces el radio (r) por π, o lo que es lo mismo, el diámetro (D) de la circunferencia por π.

El concepto “longitud de una circunferencia” es igual al del “perímetro del círculo” y miden lo mismo.

Ejercicio 1

Sea una rueda de bicicleta de radio r=30 cm. Se desea medir cuánto espacio recorre cuando la rueda da una vuelta, es decir, cual es la longitud de la circunferencia (en este caso del exterior de la rueda).

Ejercicio 2

Supongamos, para simplificar, que la Tierra es esférica y que su ecuador tiene una longitud (L) de 40.000 Km. ¿Cuál seria, en este supuesto, el radio terrestre?

A partir de la fórmula de la longitud, veamos como se relaciona el radio (r) con la longitud (L):

Ahora sustituyendo podemos calcular el radio.

Obteniendo que el radio de la Tierra es de 6.366 Km.

¿Sabías que el famoso número pi (π), (la relación entre la longitud de una circunferencia y su diámetro), ya tenia una aproximación de cinco decimales en la Babilonia del siglo XX antes de J. C.

Los matemáticos griegos intentaban resolver la cuadratura del circulo (construir un cuadrado cuya área sea igual a la de un círculo dado).

En la misma época, Arquímedes, a base de dos polígonos regulares de 96 lados, uno inscrito y otro circunscrito, llega a un valor de π = 22/7, aproximación muy importante para su época.

Después, muchos matemáticos han buscado el valor de π, hasta que Lambert, en 1768, demuestra que π es un número irracional y en 1882, Lindemann demuestra la imposibilidad de la cuadratura cel círculo.

Con la utilización de potentes ordenadores se ha llegado hasta 206 millones de decimales.

La función PI de Excel (hasta la versión actual Excel 2016) devuelve un valor de π con una aproximación de 15 decimales.

Una aproximación razonable para resolver ejercicios es π = 3,1416.